7. У вас есть 8 с виду одинаковых монет, одна из которых, тем не менее, фальшивая. Фальшивая монета чуть тяжелее, но во всем остальном идентична настоящим. У вас также есть, в лучших традициях жанра, весы с чашечками, как у богини правосудия. За какое минимальное число взвешиваний можно определить фальшивку? (популярная задача)

Решение Разбиваем монеты на три группы: 1 и 2 группы по три монеты, 3 группа - две. Взвешиваем 1 и 2 группу, если они равны, то фальшивая монета в группе 3, она находится еще за одно взвешивание (итого 2 взвешивания) Если 1 и 2 группы не равны по весу, то выбираем ту, в которой фальшивая монета (эта группа будет тяжелее), выбираем любые две монеты из группы и взвешиваем их, если получили равенство, то фальшивая монета та, которую мы не выбрали, если не получили равенства, то все просто)) итого 2 взвешивания

10. Есть три урны из тех, что содержат шары в задачках по теории вероятности. На первой написано «ЧЕРНЫЕ», на второй - «БЕЛЫЕ», на третьей - «ЧЕРНЫЕ И БЕЛЫЕ». В одной лежат белые шары, в другой - черные, в оставшейся - и черные и белые. Все надписи заведомо ложны. Разрешается достать один шар из только одной урны. Как определить в какой урне что лежит? (Microsoft)

Решение Выбираем урну с надписью “ЧЕРНЫЕ И БЕЛЫЕ” и тянем из нее шар, если вытянули белый, то в этой урне на самом деле лежат белые шары, а в урне с надписью “ЧЕРНЫЕ” лежат черные и белые шары, если вытащили черный, то в урне лежат черные шары, а в урне с надписью “БЕЛЫЕ” лежат черные и белые шары.

12. Обойти двоичное дерево, НЕ используя рекурсию. (Michael Abrash)

Решение Если в задаче разрешено использовать дополнительную память, то решение простое, с помощью стека. Пришли в вершину заносим в стек (что имено заносим и в каком порядке зависит от того, какой обход нужен: КЛП, ЛКП и т.д.)

И чем же это отличается от рекурсии? У этой задачи есть решение без использования дополнительной памяти.

Ну формально это не рекурсия, врочем, не важно, если есть другое решение будем думать)

23. Есть круглый бассейн. От его бортика в направлении точно на север отплыла рыба. Проплыв 6 метров, она опять столкнулась с бортиком. Тогда рыба повернула на восток, проплыла еще 8 метров и опять столкнулась с бортиком. Найти диаметр бассейна. (опять Мартин Гарднер)

Решение Тут все просто, если соединить начальную и конечную точку, то получится прямоугольный треугольник с катетами 6 и 8 метров, а гипотенуза будет являться диаметром (я не помню как называется этот угол образованный катетами, но этот угол в два раза меньше центрального угла опирающегося на ту же дугу, а так как он равен 90 градусов, то центральный угол 180 градусов, а следовательно дуга - полуокружность, а гипотенуза - диаметр)

25. У вас есть зажигалка и веревка. Если веревку поджечь с конца, то она вся сгорит за полчаса. Как отмерить, при помощи этих двух предметов 15 минут? Важное обстоятельство: Веревка горит неравномерно, где-то быстрее, где-то медленнее. (очень популярная задача)

Решение Поджечь с двух сторон, наверно

27. Вы стоите посреди замерзшего озера на идеально скользком льду. Трения нет вообще. Придумайте как можно больше способов добраться до берега. (Physics Mountain)

Решение Ну как минимум одно решение будет основано на законе сохранения импульса, т. е. нужно выбросить что-нибудь в сторону противоположную берегу, тогда, так как закону сохранения импульса суммарный импульс будет равен 0, мы будем двигаться к берегу. Возможны всякие неинтересные решения по типу испортить лед, чтобы получить трение. Можно также использовать реактивное движение (т. е. не бросить что-нибудь в сторону противоположную берегу, а, скажем, плюнуть (хотя наверно это тоже самое, что и выбросить), но можно еще дунуть, или извергнуть из себя еще что-нибудь ненужное)

29. В какие времена суток положение всех трех стрелок часов (часовой, минутной и секундной) совпадает? (не помню откуда)Разъяснение Часы механические, и стрелки двигаются с равномерной скоростью.

Решение Мы точно знаем, что в 00:00:00 все стрелки сходятся вместе, в следующий раз они сойдутся (грубая оценка) в интервале от 01:00:00 до 02:00:00, потом в интервале от 02:00:00 до 03:00:00 и тд, последний раз такое случится в интервале от 10:00:00 до 11:00:00 (рассматриваем только 12 часов, потому что дальше все повторяется), таким образом мы получили 11 интервалов, тогда требуемое событие происходит с периодом 1 час + 1/11 часа (12/11), зная начальное решение (00:00:00) мы можем получить все. Кстати задача имеет и строгое математическое решение, но его неудобно сюда вписывать.

20. Как провести электричество, чтобы свет на лестнице можно было включать/выключать и с верхней площадки, и с нижней. Нарисуйте схему проводки.

Решение

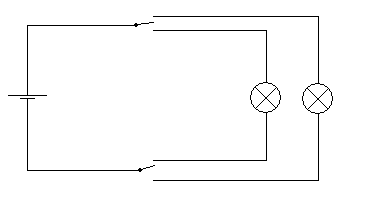Задан источник постоянного тока, но в данном случае это не важно. Свет горит, когда оба выключателя замкнуты на одну внешнюю ветвь. Должно быть решение более сложное, но с одной лампочкой (кстати лампочка обозначена чисто формально, там может быть целая система световых приборов).

Может 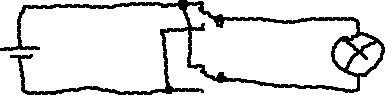? ага так, чет про более сложное решение я косанул)

4. Что делает следующий С++ код? (Matt Marcus)

.
struct A {
   A(const volatile void*);
};
 
char f(A);
int f(...);
 
template <class T>
struct Test {
   static const int value = (sizeof(f(*(T*)0)) == sizeof(char));
};

Решение *(T*) 0 - я немного не уверен в этой конструкции (как я понял, (Т*) 0 - это приведение 0 к типу T*, а первая * - это разыменование???), но в целом, (sizeof(f(*(T*)0)) - проверяет размер возвращаемого значения для функции с параметром типа Т, сравнивает с размером типа char, и таким образом, если для Т = А, то (sizeof(f(*(T*)0)) = 1, для T != A, получим (sizeof(f(*(T*)0)) = 4 (ну я принял, что sizeof(char) = 1 и sizeof(int) = 4), ну и в зависимости от того, какой тип передан в качестве T, value равно 0 или нет. Вот как-то так.